
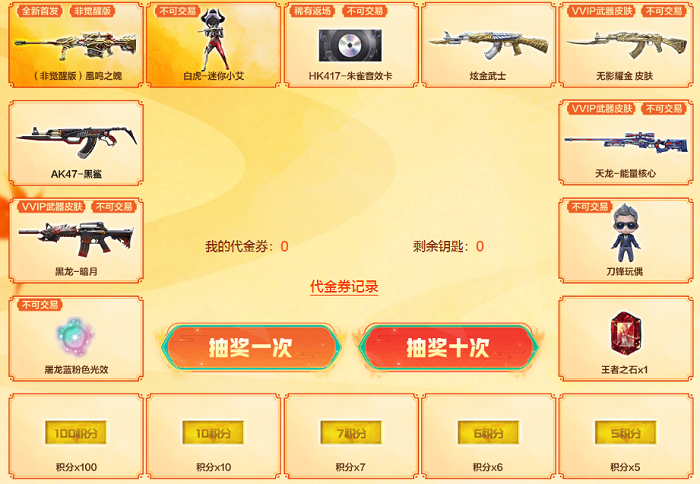
穿越火线秋枫凰鸣活动在哪里参加 穿越火线秋枫凰鸣行动活动入口地址分享
2025-04-09

崩坏星穹铁道金人旧巷客制运单怎么过 崩坏星穹铁道金人旧巷客制运单通关攻略
2025-04-09

2025-04-09

2025-04-09

2025-04-09

2025-04-09

2025-04-09

2025-04-09

2025-04-09

2025-04-09